Как начертить цилиндр в изометрии
Цилиндр — геометрическое тело, ограниченное двумя параллельными плоскостями, пересекающими цилиндрическую поверхность. Такая форма вошла во многие сферы деятельности человека: в машиностроении цилиндр одна из основных частей поршневого двигателя, в кулинарной отрасли используются инструменты цилиндрической формы, даже в моде были актуальны шляпы — цилиндры.

Инструкция
Аккуратно проведите вертикальную ось на чертежном листе. Выполняйте чертежи при помощи канцелярских инструментов — линейки, карандаша, циркуля, ластика.
Перпендикулярно построенной линии проведите две горизонтальные черты, на соответствующем высоты цилиндра расстоянии, так, чтобы эти линии делились вертикальной пополам.
Отметьте на горизонтальных линиях точки на расстоянии, равном ширине цилиндра. Их координаты на верхней и нижней линии должны совпадать, иначе построить ровный цилиндр не получится.
Отметьте на вертикальной линии ещё четыре точки, сверху и снижу от горизонтальных, отрезок между этими точками по длине должен соответствовать ширине раскрытия оснований цилиндра. В точках, лежащих на горизонтальных осях, начертите «скобки». Соедините концы этих скобок с точками на вертикальной линии. Полученные окружности являются основаниями цилиндра.
Опустите перпендикуляры от крайних точек верхней горизонтальной линии к крайним точкам нижней. Получившаяся на чертеже фигура является нужным нам цилиндром. Для законченного вида чертежа сотрите все вспомогательные линии резиновым ластиком. Основания должны быть симметричны по отношению друг к другу. Не используйте при построении шариковые ручки, маркеры, фломастеры, так как в случае неверных расчетов придется начинать работу сначала. Выполняйте все чертежи карандашом, чтобы можно было вносить корректировку в ходе построения. Данный способ – наиболее упрощенный вариант построения цилиндра, также данную фигуру вычерчивают из параллелепипеда.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Описание презентации по отдельным слайдам:
-
1 слайд
Начертательная геометрия
Проецирование цилиндра.
Построение комплексного чертежа
Построение аксонометрической проекции
Определение проекций точек на поверхности цилиндра -
2 слайд
Построение координатных осей
X
Z
Y
Y
0 -
3 слайд
Построение осей симметрии
X
Z
Y
Y
0 -
4 слайд
Построение основания цилиндра
X
Z
Y
Y
0
d -
5 слайд
Построение фронтальной и профильной проекции цилиндра
X
Z
Y
Y
0
d
h -
6 слайд
Построение круга в изометрии
Точки А- являются центрами больших дуг овала
Точки В – это центры малых дуг овала
Точки 1,2,3,4-это точки сопряжения
A
A
R=d/2
B
B
0
X
Y
1
2
3
4 -
7 слайд
Аксонометрическое изображение цилиндра
Z
Y
X
Y
0
d
Z1
X1
Y1
h
h
01
01
X1
Y1
Z1 -
8 слайд
Построение точек на поверхности цилиндра
Z
Y
X
Y
0
d
Z1
X1
Y1
h
h
a’
ZA
a
a″
ZA
a
A
01
X1
Y1
Z1
01 -
9 слайд
Построение точек на поверхности цилиндра
Z
Y
X
Y
0
d
Z1
X1
Y1
h
h
01
01
X1
Y1
Z1
b’
b
b″
ZB
XB
XB
b
ZB
B -
10 слайд
Построение точек на поверхности цилиндра
Z
Y
X
0
d
Z1
X1
Y1
h
h
01
01
X1
Y1
Z1
b’
b
b″
ZB
XB
XB
b
ZB
B
(f’)
f
f″
ZF
F
В том случае, когда
деталь включает в себя тела вращения,
приходится иметь дело с аксонометрическими
проекциями окружности.
С построением
аксонометрических проекций окружности
мы уже познакомились.
Рассмотрим примеры
построения цилиндрических и конических
тел.
Пример 1.
Построить прямой круговой цилиндр в
прямоугольной изометрии с основанием,
параллельным плоскостям проекций H,
V и W.
1. Цилиндр с
основанием, параллельным плоскости
проекций Н.
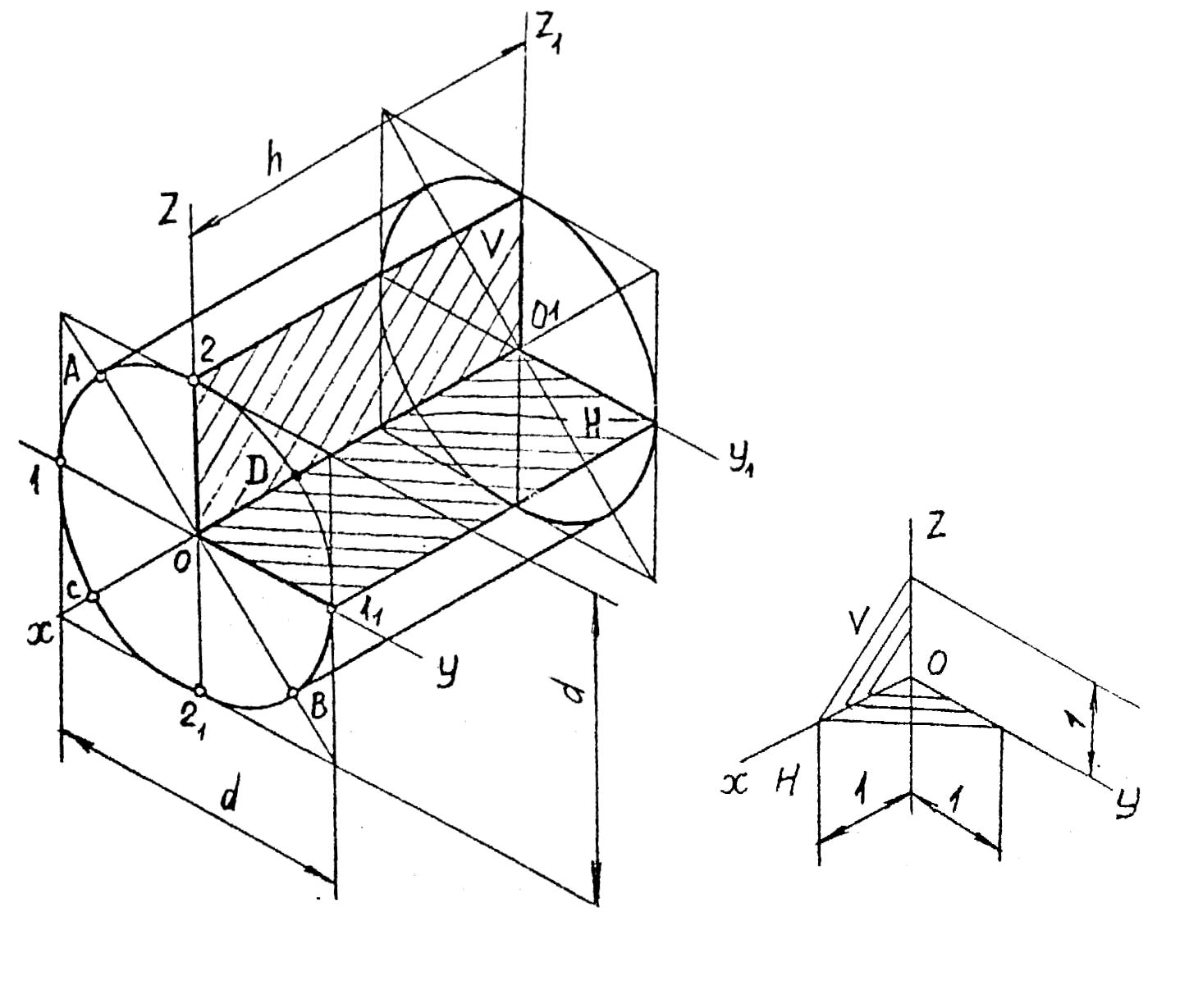
На рис. 51, а показано изображение
прямого кругового цилиндра в прямоугольной
изометрии. На осях Ох
и Оу
отложены сопряженные диаметры верхнего
основания цилиндрами через точки 1—1
и 2—2
проведены прямые, параллельные осям Ох
и Оу . В
результате получился ромб – проекция
описанного вокруг основания цилиндра
квадрата. Проекция основания цилиндра
будет представлять собой эллипс,
вписанный в ромб. Точки 1—1
и 2—2
– точки касания эллипса и ромба. Оси
эллипса совпадают с направлением
диагоналей ромба. Необходимо помнить,
что большая ось АВ
эллипса перпендикулярна оси Оz,
а малая ось CD
перпендикулярна АВ.
Величина осей эллипса:
АB
= 1,22d, СD
= 0,71d,
где d –
диаметр основания цилиндра.
Таким образом, для
построения эллипса есть 8 точек: 4 точки
касания (1—1
и 2—2)
и 4 точки – концы осей эллипса (А,
В, С,
D), АВ
и СD
– оси эллипса, 1—1
и 2—2
– сопряженные диаметры эллипса: 1—1
= 2—2
= d (диаметр
окружности).
Для построения
проекции нижнего основания цилиндра
откладывают по оси Оz
высоту цилиндра h
и через точку O1
проводят новые оси О1х1
и О1у1,
на которых повторяют построение эллипса
для нижнего основания цилиндра.
Крайние
образующие цилиндра (границы видимости)
проводят касательно к эллипсам через
точки А
и В.
Вырез производят секущими плоскостями,
совпадающими с плоскостями V
и W.
На-правление штриховки плоскостей
разреза показано на рис.
51, б.
а
б
Рис. 51
2. Цилиндр в изометрии
с основанием, параллельным плоскости
V, показан
на рис. 52, а, оси эллипса АВ
= 1,22d,
СD
= 0,71d,
АВОу,
направление штриховки плоскостей
показано на рис. 52, б.
а
б
Рис. 52
3.
Цилиндр в изометрии с основанием,
параллельным плоскости W,
показан на рис.
53, а, оси
эллипса АВ
= 1,22d,
СD
= 0,71d,
АВОх.
Направление штриховки показано на рис.
53, б.
Пример 2.
Построить прямой круговой цилиндр в
прямоугольной диметрии с основанием,
параллельным плоскостям проекций H,
V, W.
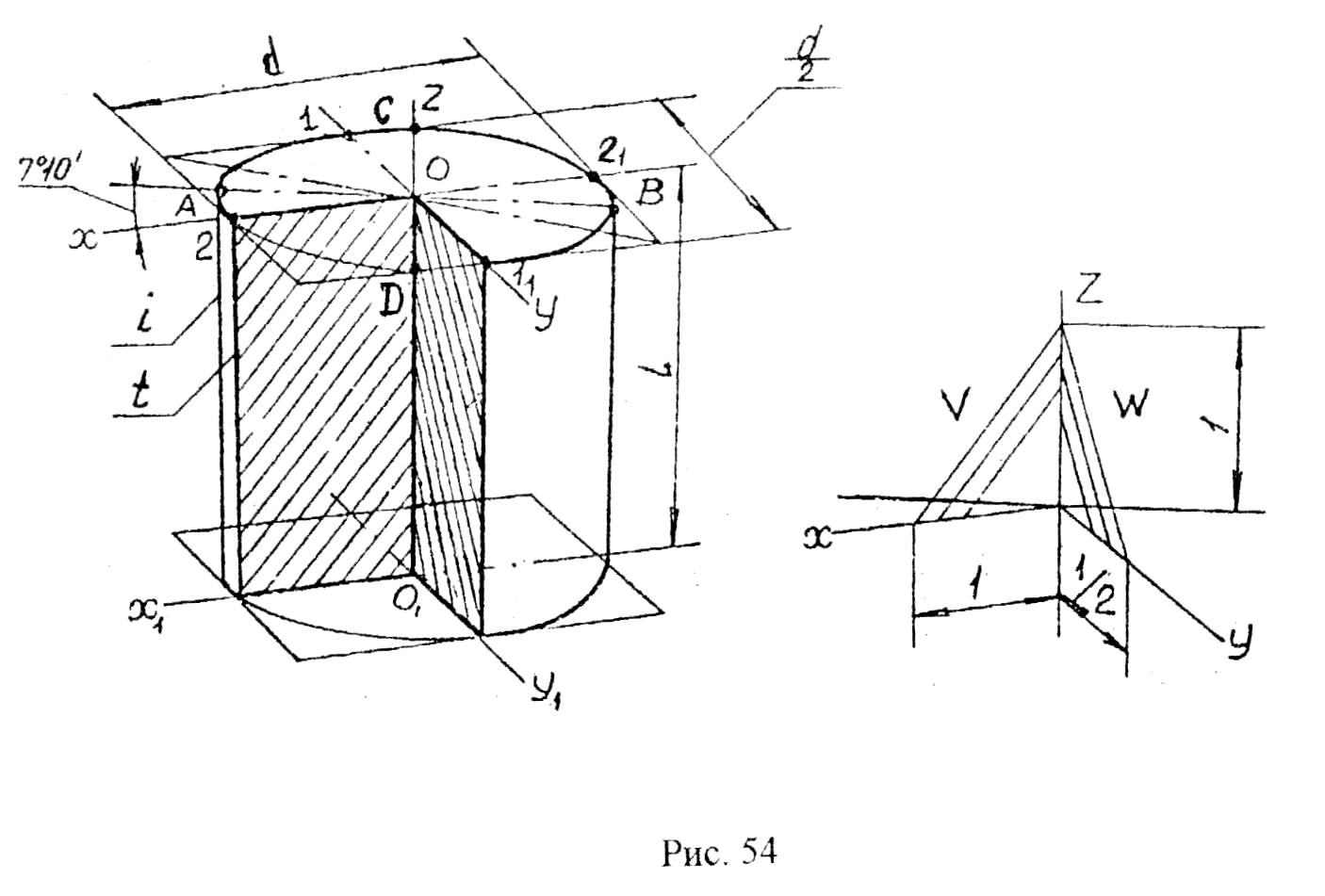
1. Цилиндр с
основанием, параллельным плоскости
проекций Н
(рис. 54). Оси эллипсов: АВ
= 1,06d, СD
= 0,35d,
АВОz.
а
б
Рис. 53
При выполнении
этой аксонометрии необходимо обратить
внимание на то, что крайняя образующая
i (граница
видимости) не совпадает с образующей t
разреза.
2. Цилиндр с
основанием, параллельным плоскости
W
(рис.
55). Оси эллипса: АВ
=1,06d, СD
= 0,35d,
АВОх.
Следует обратить внимание на несовпадение
крайней образующей i
(границей видимости) и образующей t
разреза.
Рис. 54
3. Цилиндр с
основанием, параллельным плоскости V
(рис. 56). Оси эллипса: АВ
= 1,06d, СD
= 0,95d, АВOу.
Рис. 55
Рис. 56
Пример 3.
Построить прямой круговой цилиндр во
фронтальной диметрической проекции с
основанием, параллельным плоскостям
проекций H, V,
W.
1. Цилиндр с
основанием, параллельным плоскости
V
(рис.
57). Как видно, основание проецируется
без искажения, в виде окружности диаметра
d.
Рис. 57
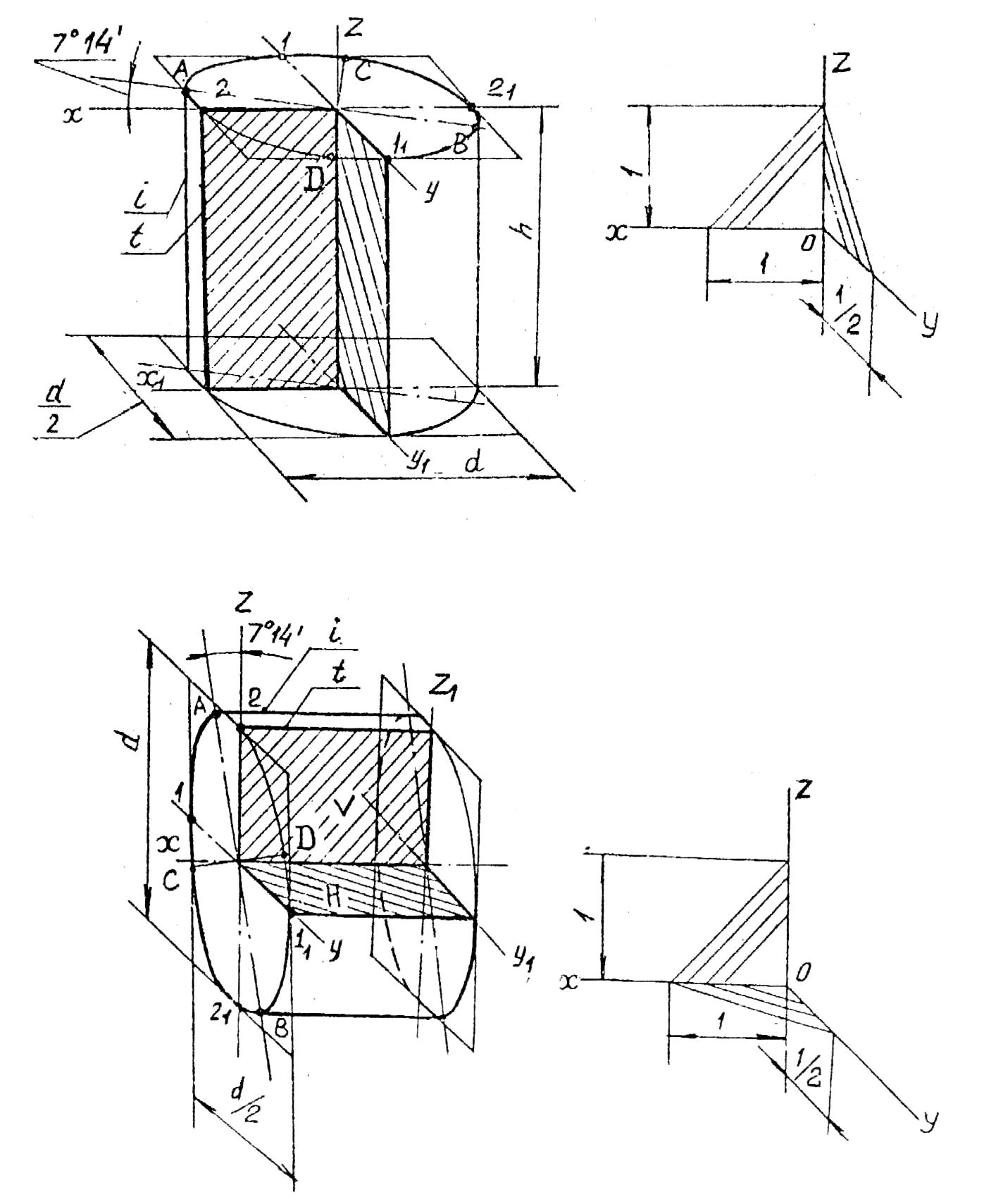
2
.
Цилиндр с основанием, параллельным
плоскости Н
(рис. 58). В
этом случае АВ =
1,07d, СD
= 0,33d, АВ
образует угол 7° 14′ с осью Ох.
Следует обратить внимание, что образующая
t разреза не
совпадает с образующей i
(границей видимости).
Рис. 58
3. Цилиндр с
основанием, параллельным плоскости W
(рис. 59). В
этом случае АВ
= 1,07d,
СD
= 0,33d,
АВ
образует угол 7″14′ с осью Оz.
Образующая
цилиндра t
, по которой проходит разрез, не совпадает
с образующей i
(границей видимости).
Рис. 59
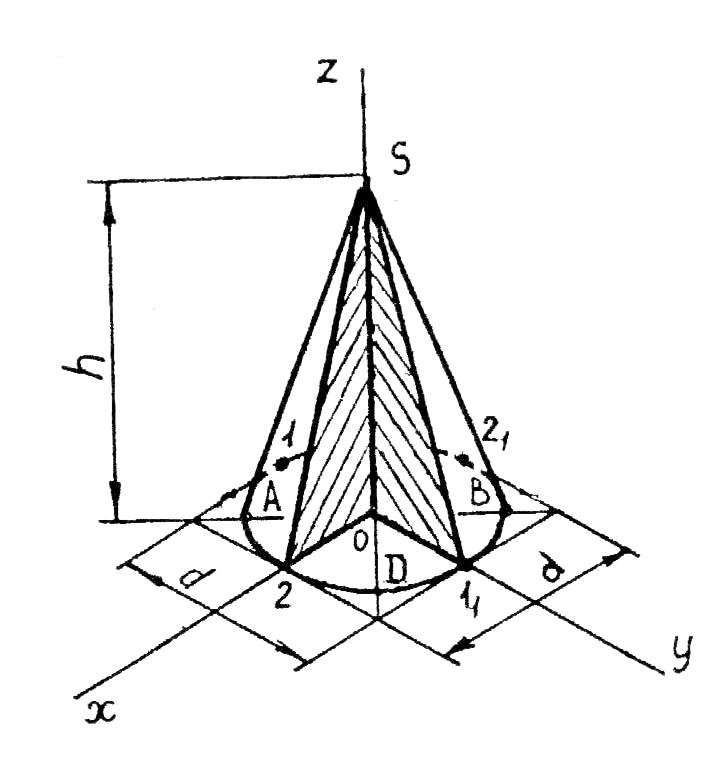
Пример 4.
Построить прямой круговой конус в
прямоугольной изометрии с основанием,
параллельным плоскости проекций H.
H
а
рис. 60 показано изображение прямого
кругового конуса в прямоугольной
изометрии. Последовательность построения
аксонометрии основания конуса аналогична
построению аксонометрии основания
цилиндра (см. рис. 51).
Рис. 60
По оси Оz
откладывают высоту конуса h,
и через вершину конуса S
проводят крайние образующие конуса
(границы видимости) касательно к эллипсу
– основанию конуса.
Вырез выполняют
секущими плоскостями, совпадающими с
плоскостями проекций V
и W.
Направление
штриховки плоскостей разреза – согласно
рис. 51, а.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Построение аксонометрического чертежа цилиндра вращения
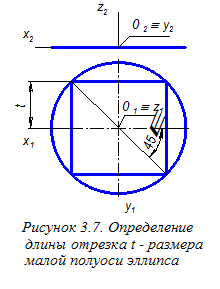
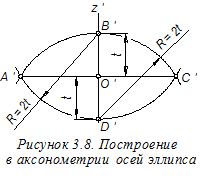
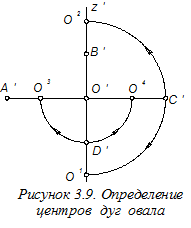
Далее на аксонометрическом чертеже (рисунок 3.8), по «свободной» оси O¢z¢, в обе стороны от начала координат О¢; отложим отрезок t и получим точки B¢; и D¢;, определяющие малую ось эллипса. Для нахождения точек А¢; и С¢;, определяющих большую ось эллипса, из найденных точек B¢; и D¢, как из центров,построим две дуги радиуса R=2t до их взаимного пересечения. Соединяя найденные точки между собой, определим большую ось эллипса.
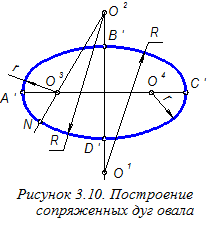
R =О1В¢ = О2D¢; r = О3А¢ = О4С¢; (рисунок 3.10). Далее из найденных центров О1, О2, О3, О4 циркулем строим четыре сопряжённые дуги овала. Напомним, что точка сопряжения двух дуг располагается на прямой, проходящей через центры этих дуг. Например, точка N сопряжения нижней дуги радиуса R с левой дугой радиуса r находится на прямой, проходящей через центры
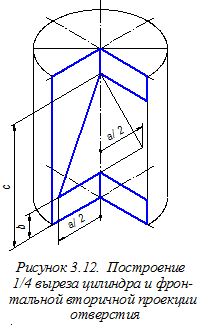
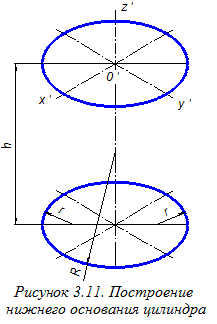
Аксонометрию нижнего основания цилиндра строим смещением вниз на величину h центров О1, О2, О3, О4 дуг овала верхнего основания (рисунок 3.11). Далее строим ¼ часть выреза цилиндра и изображаем фронтальную вторичную проекцию призматического отверстия, образованного плоскостями a, b и g (рисунок 3.12). Размеры a, b и с, необходимые для этого переносим на аксонометрический чертёж из ортогонального чертежа (см. рисунок 3.2) параллельно соответствующим аксонометрическим осям.
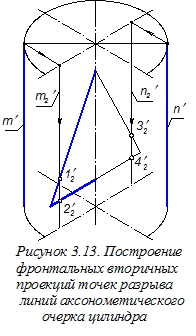
Обозначим через m¢; и n¢; аксонометрические очерковые образующие цилиндра (рисунок 3.13) и построим их фронтальные вторичные проекции m¢2 и n¢2 (последовательность построений показана стрелками). Далее отметим точки 12¢, 22¢, 32¢, 42¢ — пересечение линий фронтальной вторичной проекции отверстия в цилиндре с фронтальными вторичными проекциями линий аксонометрического очерка и находим точки 1¢, 2¢, 3¢, 4¢ разрыва линий m¢ и n¢ — аксонометрических очерковых образующих конуса граничными линиями отверстия в нём (рисунок 3.14).
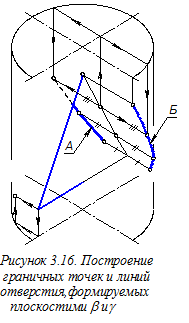
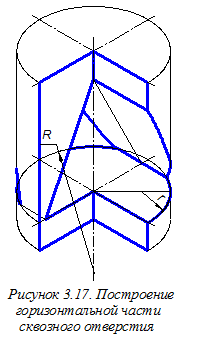
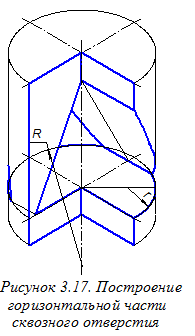
Строим овал, определяющий горизонтальную часть призматического отверстия в цилиндре, формируемую плоскостью a (рисунок 3.17). Для этого можно использовать дуги R и r овала верхнего основания конуса, найдя новые центры этих дуг. У построенного овала сохраняем лишь те его участки, которые видны в аксонометрии.

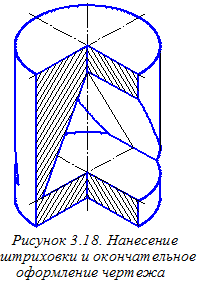
Подчеркнём, что окончательное оформление аксонометрического чертежа рассматриваемого цилиндра требует плавного соединения всех полученных точек при изображении сквозного отверстия и обводку всех видимых линий контура изображения цилиндра.
3.4. Построение ортогонального и аксонометрического чертежей
конуса вращения
Переходим к рассмотрению в задаче 2 построения ортогонального и аксонометрического чертежей конуса вращения.
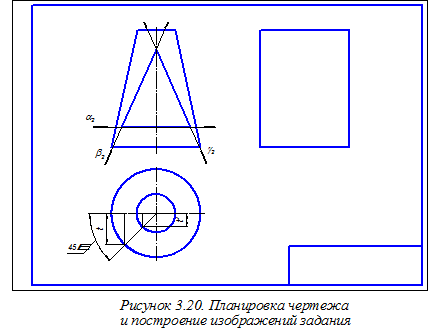
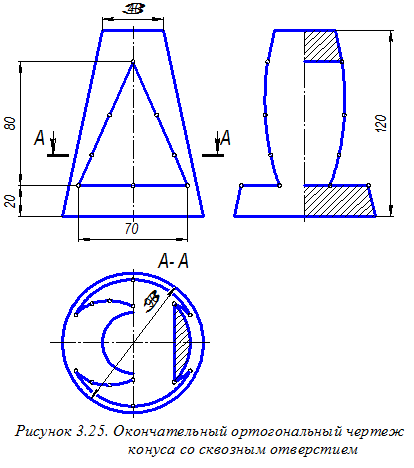
На рисунке 3.20 показаны изображения: главный вид и частично вид сверху прямого кругового усечённого конуса, а также габаритный прямоугольник для последующего построения вида слева.
Рассматриваемый конус имеет сквозное отверстие, образованное тремя плоскостями: горизонтальной плоскостью a, рассекающей коническую поверхность по окружности, и двумя фронтально проецирующими плоскостями b и g, рассекающими его поверхность по эллипсам.
Для построения видов сверху и слева, а также аксонометрического изображения данного конуса осуществим привязку этой фигуры к прямоугольной системе координат Оxyz (рисунок 3.21). В качестве горизонтальной координатной плоскости выберем плоскость нижнего основания конуса.
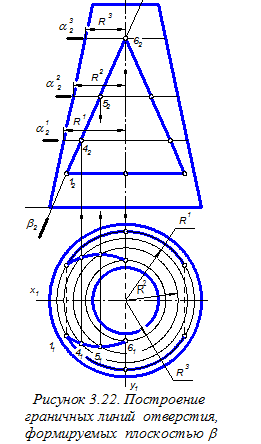

Аналогично определяем горизонтальные проекции точек 4, 5 и 6 граничных линий отверстия, расположенных в плоскости b (рисунок 3.22). Для этого строим окружности радиуса R 1, R 2 и R 3, расположенные в промежуточных горизонтальных плоскостях a 1, a 2, a 3.
Аналогично строим на виде сверху точки граничных линий отверстия, расположенных в плоскости g. Последовательно соединяем найденные горизонтальные проекции точек плавными кривыми. Окончательное оформление вида сверху показано на рисунке 3.23. Здесь линиями невидимого контура показаны линии пересечения плоскостей a и b, g и b, a и g.
Построение профильных проекций рассматриваемых точек (см. рисунок 3.23) осуществляем как по линиям связи (точки 33 и 63) на линиях профильного очерка конуса, так и переносом отрезков ординат точек с вида сверху на вид слева. Переносимые отрезки показаны одинаковыми символами как на виде сверху, где они измеряются, так и на виде слева, где они откладываются. Последовательно соединяем найденные профильные проекции точек
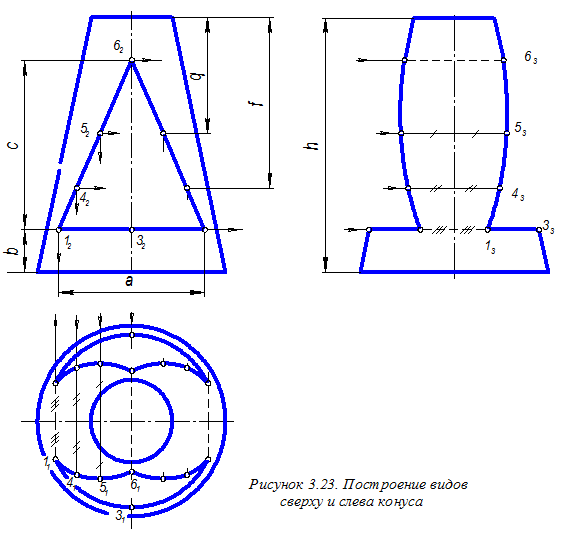 |
плавной кривой, а также изображаем линии невидимого контура, определяющие линии пересечения плоскостей a и b,
g и b, a и g.
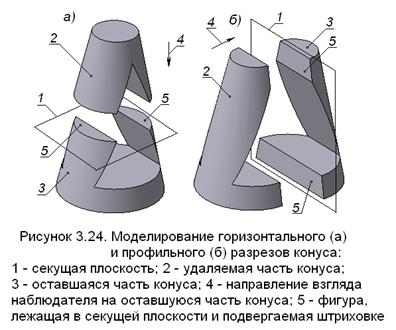
Более подробная информация о правилах построения и обозначения разрезов в соответствии с ГОСТ 2.305 – 68 приведена в разделе 3.2.
 |
Построим прямоугольную изометрическую проекцию рассматриваемого конуса, используя привязку к нему ортогональной системы координат Оxyz, выполненную ранее (см. рисунок 3.21). На отдельном листе ватмана формата А3 или А4 изобразим аксонометрические оси (см. рисунок 2.4).
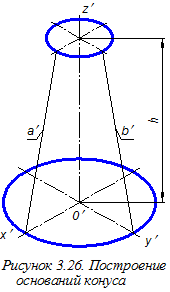
Далее построим аксонометрические проекции окружностей нижнего и верхнего оснований конуса. Такими проекциями будут два эллипса, центры которых располагаются на координатной оси O¢z¢; и смещены относительно друг друга на расстояние h (рисунок 3.26). Эллипсы имеют следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, — где d — диаметр изображаемой окружности. Малая ось эллипсов располагается вдоль «свободной» координатной оси O¢z¢;, а её размер равен длине стороны квадрата, вписанного в изображаемую окружность.
Для удобства построений вместо эллипсов изображаем овалы (см. рисунки 3.9 и 3.10). При этом используем графическое определение как малых полуосей эллипсов (см. на рисунке 3.20, на виде сверху отрезки t и t¢), так и больших полуосей (см. рисунок 3.8).
Далее строим прямые m¢; и n¢, являющиеся аксонометрическим очерком конической поверхности (рисунок 3.27). При этом определяем точки касания этими линиями эллипсов, являющихся основаниями конуса. Для этого удлиняем образующие а¢; и b¢ до точек А¢; и В¢; пересечения этих линий с верхним основанием конуса. Образующие а¢; и b¢ вместе с осевой линией чертежа образуют три прямые, проходящие через вершину конyса. Эта вершина на чертеже недоступна. Указанные три прямые пересекают эллипсы (овалы) оснований в шести точках. Соединяем точки пересечения с 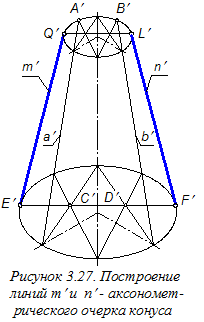
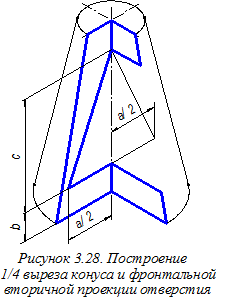

существу строим фронтальные вторичные проекции плоскостей a, b и g, формирующих отверстие в конусе (рисунок 3.28). При этом размеры a, b и c из ортогонального чертежа (см. главный вид на рисунке 3.23) переносим на аксонометрический чертёж параллельно соответствующим аксонометрическим осям.
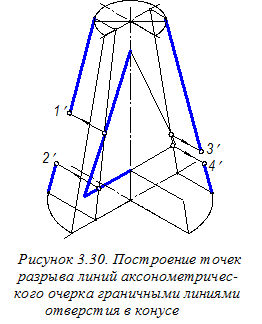
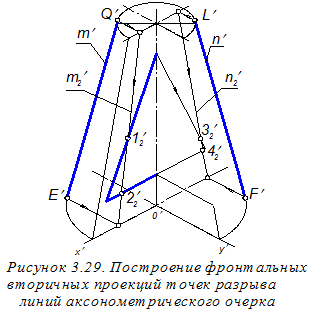
Далее необходимо построить точки 1¢, 2¢, 3¢ и 4¢; разрыва линий аксонометрического очерка конуса граничными линиями отверстия в нём. Однако перед этим предварительно определим их фронтальные вторичные проекции 12¢, 22¢, 32¢, 42¢ (рисунок 3.29). Для этого сначала строим фронтальные вторичные проекции m2¢, n2¢ очерковых образующих конуса и находим точки пересечения этих проекций с линиями вторичной проекции отверстия. Последовательность этих построений показана стрелками. При этом подчеркнём, что построения начинаются не в конечных точках больших осей эллипсов (овалов), а в граничных точках E¢;, F¢, Q¢;, L¢; аксонометрических очерковых образующих, построенных ранее. Далее находим искомые точки 1¢, 2¢, 3¢ и 4¢; (рисунок 3.30).
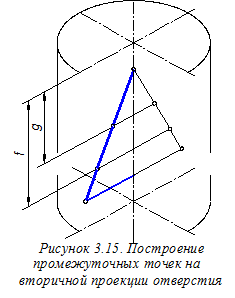
Строим аксонометрические проекции промежуточных точек граничных линий отверстия. Для этого сначала на линиях фронтальной вторичной проекции отверстия намечаем промежуточные точки (рисунок 3.31). При этом используем размеры g и f, перенося их из ортогонального чертежа (см. рисунок 3.23). Далее через найденные вторичные проекции проводим прямые, параллельные оси О¢у¢;, и откладыванием на них в обе стороны ординаты искомых 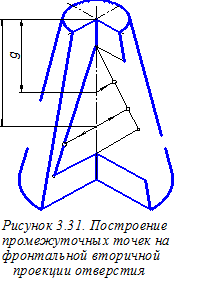
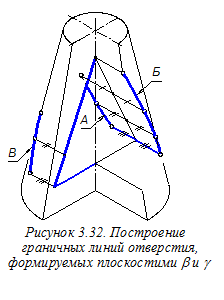
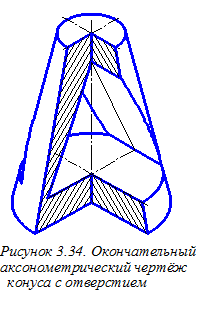
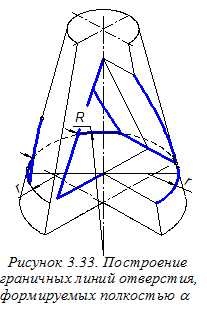
Выполняем штриховку участков конуса, расположенных в координатных плоскостях хОz и уОz. Определение направлений линий штриховки в прямоугольной изометрии показано на рисунке 3.19.
Окончательное оформление аксонометрического чертежа конуса со сквозным отверстием (рисунок 3.34) требует тщательной обводки всех линий изображения: дуги овалов обводятся циркулем, а другие кривые – с помощью лекала.
4. Построение ортогонального и аксонометрического чертежей детали
(третья задача)
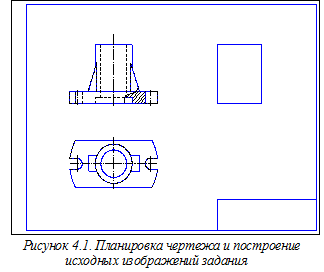
Планировка листа и построение изображений детали по размерам, нанесённым на эти изображения в индивидуальном задании, показаны на рисунке 4.1. Изображения включают в себя: главный вид, вид сверху, а также габаритный прямоугольник для дальнейшего построения вида слева.
Для построения вида слева и аксонометрического чертежа детали осуществим привязку детали к прямоугольной системе координат О xyz (рисунок 4.2). За горизонтальную координатную плоскость примем плоскость верхнего основания цилиндрической плиты, срезанной по бокам двумя фронтальными плоскостями, и имеющей два полуовальных выреза. На этой плите расположен цилиндр вращения, ось которого совпадает с координатной осью Оz. Его подкрепляют два ребра жёсткости – призматические элементы треугольной формы. Внутренняя форма детали состоит из сквозного ступенчатого цилиндрического отверстия.
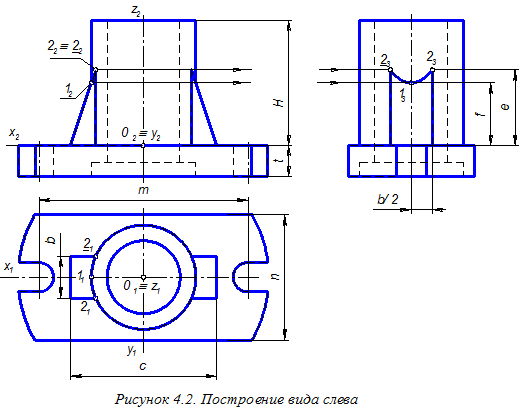
В третьей задаче кроме видов необходимо построить фронтальный и профильный разрезы детали. Так как рассматриваемая деталь имеет две плоскости симметрии: фронтальную и профильную, — и по этим плоскостям выполняется её рассечение, то положение секущих плоскостей на чертеже не указываем, а разрезы совмещаем с половинами соответствующих видов (рисунок 4.3). Границей между этими изображениями является ось симметрии (штрих пунктирная линия). Вид оставляем слева от осевой линии, а разрез помещаем справа от этой линии. При выполнении разрезов удаляем все линии, изображающие внешнюю форму детали, а линии невидимого контура (штриховые линии) заменяем сплошными основными линиями. На всех видах удаляем штриховые линии. Контуры детали, расположенные в секущих плоскостях, заштриховываем тонкими параллельными линиями, расположенными под углом 45° к линиям основной надписи чертежа. Направление штриховки должно быть одинаковым для всех выполненных разрезов. Рекомендуется соблюдать интервал штриховки, равный 2,5 … 3 мм.
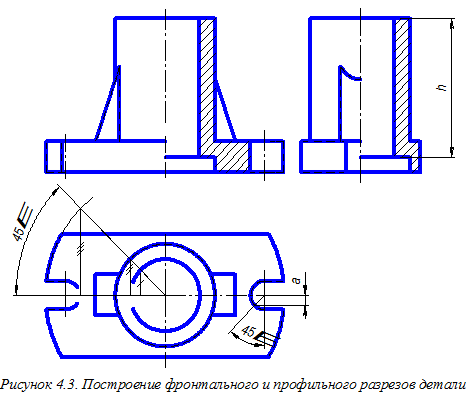 |
Обращаем внимание на условность, принятую в машиностроительном черчении, — при продольном разрезе ребра жёсткости его контур не заштриховывается. Более подробная информация о разрезах приведена в подразделе 3.2.
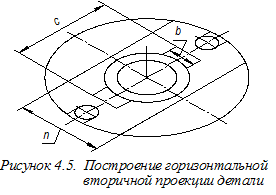 |
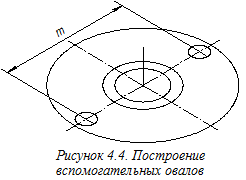
Напомним, что круглое основание любого цилиндрического или конического элемента детали, расположенное в координатной плоскости или параллельно такой плоскости, в прямоугольной изометрии изображается эллипсом, имеющим следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, — где d — диаметр изображаемой окружности. Малая ось эллипсов располагается вдоль «свободной» координатной оси, — оси, перпендикулярной плоскости, в которой расположена изображаемая окружность,а размер малой оси равен длине стороны квадрата, вписанного в изображаемую окружность. Для удобства построения и получения лучшего качества изображения на аксонометрическом чертеже вместо эллипсов строим овалы – циркульные кривые (см. рисунки 3.9 и 3.10). Поэтому сначала строим овалы, определяющие горизонтальные вторичные проекции всех цилиндрических элементов детали (рисунок 4.4). Для графического определения малых полуосей эллипсов используем построения, показанные на рисунке 4.3 (см. размер а и отрезки, помеченные штрихами). Размеры b, c, m и n, используемые для построений, переносим с ортогонального чертежа (см. рисунок 4.2).Далее строим прямые, определяющие горизонтальные вторичные проекции плоских элементов детали (рисунок 4.5). На следующем этапе построения аксонометрии удаляем ненужные линии чертежа с учётом выполнения в дальнейшей выреза ¼ детали (рисунок 4.6).
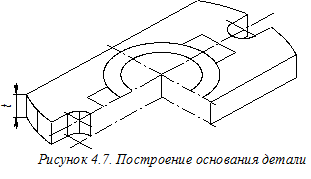 |
Далее создадим объёмное изображение основания детали (рисунок 4.7). Для этого из точек горизонтальной вторичной проекции основания детали, расположенных ближе к наблюдателю, строим вспомогательные прямые, параллельные оси О¢ z¢, и на них откладываем вниз отрезки длиной t, определяющей толщину плиты основания. Таким образом, определяем точки контура нижней части основания. Изображения плоских участков основания выполняем лишь по их граничным точкам, а для цилиндрических участков строим и промежуточные точки. Длину отрезка t определяем на ортогональном чертеже (см. рисунок 4.2). Соединяя найденные точки нижней плоскости основания прямыми или плавными кривыми и удаляя ненужные вспомогательные вертикальные отрезки, построим основание детали.
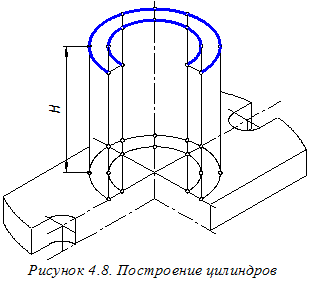
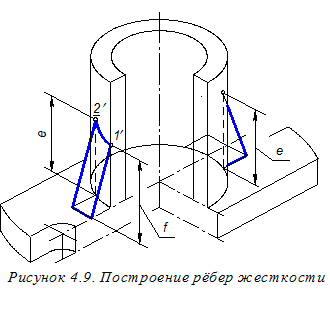
Аналогично с помощью вспомогательных вертикальных отрезков длиной Н, используя горизонтальные вторичные проекции цилиндрических элементов, можно построить точки верхнего основания этих элементов детали (рисунок 4.8). Найденные точки соединяем плавными кривыми, а вспомогательные вертикальные отрезки и невидимые линии чертежа удаляем. Для построения изображения рёбер жёсткости находим точки 1¢; и 2 ¢; (рисунок 4.9). Для этого из соответствующих точек горизонтальных вторичных проекций рёбер строим вспомогательные вертикальные отрезки длиной е и f. Длины этих отрезков измеряем на ортогональном чертеже (см. рисунок 4.2). Строим лишь видимые элементы рёбер, а невидимые удаляем.
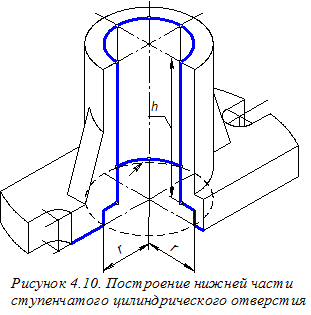
Для изображения в аксонометрии видимой части окружности радиуса r цилиндрического углубления, расположенного в нижней части детали, строим образующие этой цилиндрической поверхности, попадающие в вырез ¼ части детали и овал, соответствующий окружности цилиндрического углубления, расположенной в нижней плоскости основания детали (см. на рисунке 4.10 овал, изображённый штриховой линией). У построенного овала сохраняем 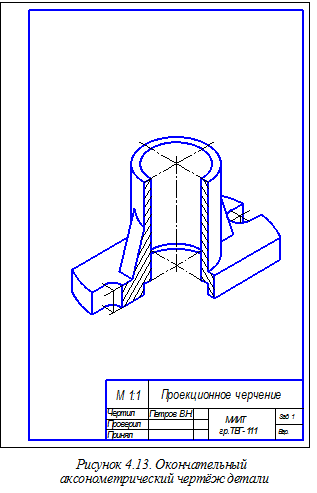
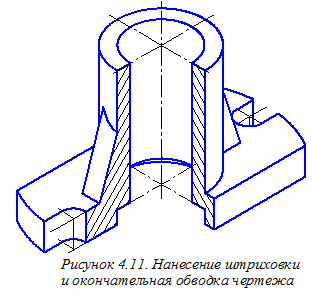
В заключение производим обводку чертежа и наносим штриховку (рисунок 4.11). Определение направлений линий штриховки в аксонометрии показано на рисунке 3.19.
Окончательное оформление аксонометрического чертежа детали требует плавного (с помощью лекал) соединения построенных точек кривых линий, изображающих как элементы сквозного ступенчатого цилиндрического отверстия в детали, так и элементы её внешней формы. Завершается оформление чертежа заполнением его основной надписи.
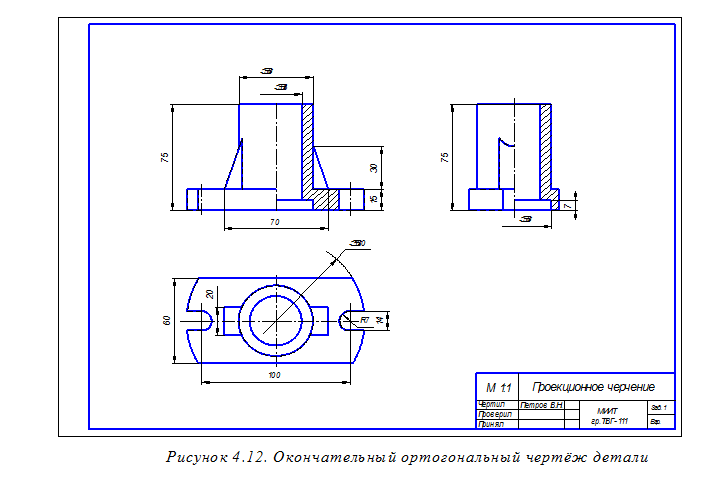
Окончательно оформленные ортогональный и аксонометрический чертежи детали показаны соответственно на рисунках 4.12 и 4.13.
Отметим также, что во всех рассмотренных ранее построениях измерение размеров на ортогональном чертеже и перенос их на аксонометрический чертеж производилось с помощью измерителя.
На изображениях ортогонального и аксонометрического чертежей рекомендуется сохранять характерные и вспомогательные точки построенных линий, без обозначения этих точек.
Литература
1. Единая система конструкторской документации. Общие правила выполнения чертежей. М., 1991,453 с.
2. Аверин В.Н., Куколева И Ф. Нанесение размеров на чертежах. Методические указания к практическим занятиям по инженерной графике. М.: МИИТ, 2008. 37 с.
3. Аверин В.Н., Пуйческу Ф.И. Прямоугольная изометрическая проекция. Методические указания к практическим занятиям по инженерной графике. М.: МИИТ, 2008. 23 с.
Учебно-методическое издание
|
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил… |
Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах… |
Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют… |